stochastics

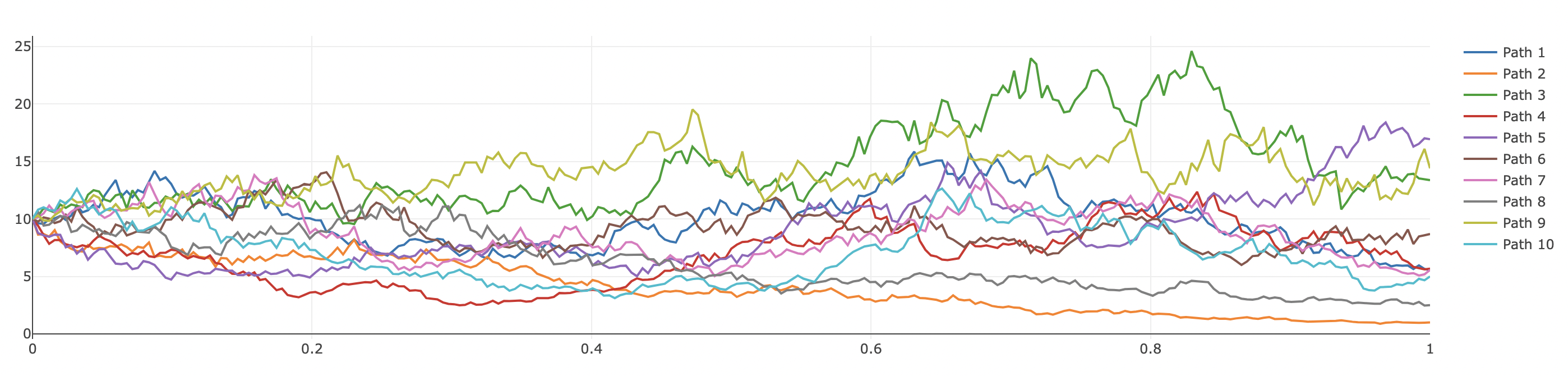
Many stochastic processes can be generated:

// Run this example using:
//      cargo run --example stochastic_processes
//
// This example generates paths for each stochastic process
// and plots them using the `plotters` crate.
//
// See the ./images/ directory for the output.

use RustQuant::stochastics::*;
use RustQuant::utils::plot_vector;

const INITIAL_VALUE: f64 = 10.0;
const START_TIME: f64 = 0.0;
const END_TIME: f64 = 1.0;
const NUM_STEPS: usize = 252;
const NUM_SIMS: usize = 1;
const PARALLEL: bool = false;

#[rustfmt::skip]
fn main() {
    // Create new stochastic processes.
    let abm = ArithmeticBrownianMotion::new(0.05, 0.9);
    let bdt = BlackDermanToy::new(0.13, 0.1);
    let bm = BrownianMotion::new();
    let cir = CoxIngersollRoss::new(0.05, 0.9, 0.1);
    let ev = ExtendedVasicek::new(0.05, 2.0, 0.1);
    let gbm = GeometricBrownianMotion::new(0.05, 0.9);
    let hl = HoLee::new(0.2, 0.1);
    let hw = HullWhite::new(0.1, 0.2, 0.1);
    let ou = OrnsteinUhlenbeck::new(0.05, 0.9, 0.1);
    let fbm = FractionalBrownianMotion::new(0.7, FractionalProcessGeneratorMethod::FFT);
    let mjd = MertonJumpDiffusion::new(0.05, 0.5, 30.0, 0.0, 5.0);
    let gbb = GeometricBrownianBridge::new(0.05, 0.9, INITIAL_VALUE, END_TIME);
    let cev = ConstantElasticityOfVariance::new(0.05, 0.9, f64::sin);

    // Generate path using Euler-Maruyama scheme.
    // Parameters: x_0, t_0, t_n, n, sims, parallel.
    let config = StochasticProcessConfig::new(INITIAL_VALUE, START_TIME, END_TIME, NUM_STEPS, NUM_SIMS, PARALLEL);

    let abm_out = abm.euler_maruyama(&config);
    let bdt_out = bdt.euler_maruyama(&config);
    let bm_out  = bm.euler_maruyama(&config);
    let cir_out = cir.euler_maruyama(&config);
    let ev_out  = ev.euler_maruyama(&config);
    let gbm_out = gbm.euler_maruyama(&config);
    let hl_out  = hl.euler_maruyama(&config);
    let hw_out  = hw.euler_maruyama(&config);
    let ou_out  = ou.euler_maruyama(&config);
    let fbm_out = fbm.euler_maruyama(&config);
    let mjd_out = mjd.euler_maruyama(&config);
    let gbb_out = gbb.euler_maruyama(&config);
    let cev_out = cev.euler_maruyama(&config);

    // Plot the paths.
    plot_vector!(abm_out.paths[0].clone(), "./images/arithmetic_brownian_motion.png");
    plot_vector!(bdt_out.paths[0].clone(), "./images/black_derman_toy.png");
    plot_vector!(bm_out.paths[0].clone(),  "./images/brownian_motion.png");
    plot_vector!(cir_out.paths[0].clone(), "./images/cox_ingersoll_ross.png");
    plot_vector!(ev_out.paths[0].clone(),  "./images/extended_vasicek.png");
    plot_vector!(gbm_out.paths[0].clone(), "./images/geometric_brownian_motion.png");
    plot_vector!(hl_out.paths[0].clone(),  "./images/ho_lee.png");
    plot_vector!(hw_out.paths[0].clone(),  "./images/hull_white.png");
    plot_vector!(ou_out.paths[0].clone(),  "./images/ornstein_uhlenbeck.png");
    plot_vector!(fbm_out.paths[0].clone(), "./images/fractional_brownian_motion.png");
    plot_vector!(mjd_out.paths[0].clone(), "./images/merton_jump_diffusion.png");
    plot_vector!(gbb_out.paths[0].clone(), "./images/geometric_brownian_bridge.png");
    plot_vector!(cev_out.paths[0].clone(), "./images/constant_elasticity_of_variance.png");

    plot_trajectories(&gbm_out, true);
}

Paths can be plotted via the plot_vector! macro or plotly: