
RustQuant is a Rust library (crate) for quantitative finance.
Code
The crate is available for download from Crates.io, and the source is available on GitHub.
Installation
RustQuant of course requires Rust to be installed first.
You can easily add RustQuant to your Rust project by running:
cargo add RustQuant
Documentation
API documentation can be found at Docs.rs.
The documentation contained in this book is more "cookbook" style.
Contributions to documentation in any form are highly welcome.
Note: this book is a very early work-in-progress and has almost no content.
autodiff
The autodiff module can be used to differentiate scalar output functions of the form:
\[f : \mathbb{R}^n \rightarrow \mathbb{R} \]
Simple expressions are differentiated as follows:
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
// SIMPLE EXPRESSIONS
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
let g = Graph::new();
let a = 1.;
let b = 2.;
let x = g.var(69.);
let y = g.var(420.);
// Define a function.
let f = a + b + (x * y).exp();
// Accumulate the gradient.
let gradient = f.accumulate();
println!("z = {}", f.value);
println!("dz/dx = {}", gradient.wrt(&x));
println!("dz/dy = {}", gradient.wrt(&y));
println!("grad = {:?}", gradient.wrt(&[x, y]));
Block expressions are also supported:
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
// BLOCK EXPRESSIONS
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
let g = Graph::new();
let x = g.var(69.);
let y = g.var(420.);
let block = {
let z = x.sin() + y.tan();
z.exp()
};
let grad = block.accumulate();
println!("f = {}", block.value);
println!("df/dx = {}", grad.wrt(&x));
println!("df/dy = {}", grad.wrt(&y));
println!("grad = {:?}", grad.wrt(&[x, y]));
Closures and functions are also supported:
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
// CLOSURES
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
let g = Graph::new();
let x = g.var(1.);
let y = g.var(2.);
let closure = || (x * y).cosh() / (x.tanh() * y.sinh());
let grad = closure().accumulate();
println!("z = {}", closure().value);
println!("dz/dx = {}", grad.wrt(&x));
println!("dz/dy = {}", grad.wrt(&y));
println!("grad = {:?}", grad.wrt(&[x, y]));
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
// PROPER FUNCTIONS.
//
// Note that you can also add many variables via vectors, slices, arrays, etc.
// This is where the `autodiff` crate really shines, as it allows
// you to differentiate functions of any number of variables and
// computing gradients for large functions using AD rather than
// finite-difference quotients is significantly faster and has no error.
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
// Function to differentiate:
// f = x^(y + cos(1)) - atanh(z) / 2 + 1
// at x = 3, y = 2, z = 1.
#[rustfmt::skip]
fn function<'v>(variables: &[Variable<'v>], constants: &[f64]) -> Variable<'v> {
variables[0].powf(variables[1] + constants[0].cos()) -
variables[2].atanh() / constants[1] +
constants[0]
}
// New graph.
let graph = Graph::new();
// Variables and constants.
let variables = graph.vars(&[3.0, 2.0, 1.0]);
let constants = [1., 2.];
// Evaluate and differentiate the function.
let result = function(&variables, &constants);
let gradient = result.accumulate();
// Print the graph length.
println!("Graph length: {}", graph.len());
println!("{:?}", gradient.wrt(&variables));
// Print the graphviz output.
// You can copy and paste this into your Graphviz viewer of choice.
println!("{}", graphviz(&graph, &variables));
data
The data module encompasses everything data related.
That is, anything that can be observed, either in markets or derived from market observable data, and also facilities to manage that data.
Another form of data is contextual (or reference) data. These are things such as calendars and date conventions. While there are facilities to handle these data inside the data module, the underlying implementations are in other modules, such as the time module.
Curves
Curves can be fit to market data. Here we include an example of a spot curve being fitted.
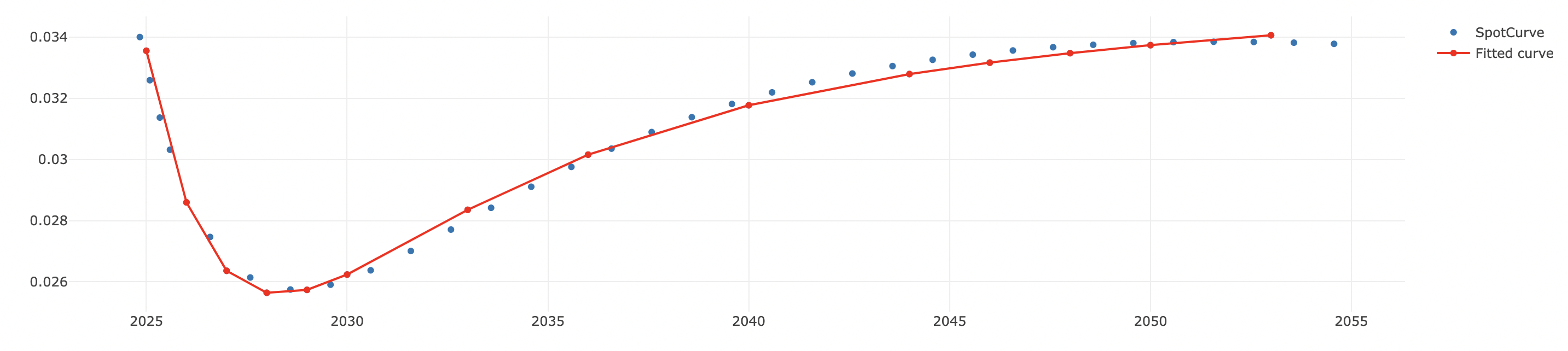
#![allow(unused)] fn main() { {{#include ../../../examples/examples/curves_spot.rs}} }
instruments
European Vanilla Options
To price a vanilla European option, we begin by defining the option itself:
// Define the option contract.
let option = EuropeanVanillaOptionBuilder::default()
.strike(100.0)
.expiry(date!(2025 - 12 - 31))
.type_flag(TypeFlag::Call)
.build()?;Then we need to define a model to price the option with:
// Define some models to price the option.
let bs73 = BlackScholes73::new(100., 0.05, 0.2);
let m73 = Merton73::new(100., 0.05, 0.03, 0.2);
let b76 = Black76::new(100., 0.05, 0.2);
let a82 = Asay82::new(100., 0.2);
let gk83 = GarmanKohlhagen83::new(100., 0.05, 0.03, 0.2);
let h93 = Heston93::new(100., 0.05, 0.03, 0.2, 0.1, 0.1, 0.1, 0.1);
let bch = Bachelier::new(100., 0.05, 0.2);Lastly, we construct an AnalyticOptionPricer, from which we can generate a report.
The report simply prints the option, model, price, and Greeks.
// Print the option, model, price and greeks.
AnalyticOptionPricer::new(option, bs73).report();
AnalyticOptionPricer::new(option, m73).report();
AnalyticOptionPricer::new(option, b76).report();
AnalyticOptionPricer::new(option, a82).report();
AnalyticOptionPricer::new(option, gk83).report();
AnalyticOptionPricer::new(option, h93).report();
AnalyticOptionPricer::new(option, bch).report();The output will look something like this:
// Model: BlackScholes73 { s: 100.0, r: 0.05, v: 0.2 }
// Option: EuropeanVanillaOption { strike: 100.0, expiry: 2025-12-31, type_flag: Call }
// {
// "theta": -6.21680948799122,
// "vega": 39.12469842218203,
// "charm": 0.06220900042967281,
// "zomma": -0.0837348839459069,
// "price": 11.08579175284256,
// "lambda": 5.802560832438351,
// "rho": 58.59700502681849,
// "delta": 0.6432598102161233,
// "vanna": -0.2934352381663651,
// "speed": -0.0004887850033760005,
// "color": 0.009163226593140452,
// "gamma": 0.01777400012276366,
// "vomma": 11.303583301850122,
// "ultima": -160.90535329601363,
// }
// Model: Merton73 { s: 100.0, r: 0.05, q: 0.03, v: 0.2 }
// Option: EuropeanVanillaOption { strike: 100.0, expiry: 2025-12-31, type_flag: Call }
// {
// "theta": -4.272756285502488,
// "gamma": 0.017995444677726104,
// "zomma": -0.08997722338863051,
// "speed": -0.0003599088935545221,
// "color": 0.009074941597741354,
// "delta": 0.5641575465829798,
// "ultima": -43.59776593173644,
// "price": 9.092954864173855,
// "rho": 52.084231395586315,
// "vanna": 5.2399933461312134e-17,
// "charm": 0.01906616295796282,
// "vega": 39.6121492700665,
// "vomma": -1.1534441205446944e-15,
// "lambda": 6.204336819109864,
// }
// Model: Black76 { f: 100.0, r: 0.05, v: 0.2 }
// Option: EuropeanVanillaOption { strike: 100.0, expiry: 2025-12-31, type_flag: Call }
// {
// "zomma": -0.09046830043585345,
// "speed": -0.00026845029437156125,
// "vomma": -2.1679251440048266,
// "ultima": 10.958928376819475,
// "color": 0.009114622059396617,
// "gamma": 0.017896686291437418,
// "vanna": 0.19697379573327434,
// "theta": -3.183941196979144,
// "delta": 0.5127676040720752,
// "vega": 39.394759146654856,
// "rho": 47.7324390165048,
// "price": 7.907921226166792,
// "charm": -0.007741693912166335,
// "lambda": 6.4842275157643305,
// }
// Model: Asay82 { f: 100.0, v: 0.2 }
// Option: EuropeanVanillaOption { strike: 100.0, expiry: 2025-12-31, type_flag: Call }
// {
// "ultima": 11.578909557862003,
// "theta": -3.7818316687297053,
// "rho": 50.4328138066247,
// "vega": 41.62344506035159,
// "vanna": 0.208117225301758,
// "gamma": 0.018909158343648525,
// "charm": 0.018909158343648536,
// "lambda": 6.48422751576433,
// "zomma": -0.0955863778447514,
// "speed": -0.0002836373751547279,
// "color": 0.008684807091491406,
// "price": 8.355297299155879,
// "delta": 0.5417764864957794,
// "vomma": -2.290571514614832,
// }
// Model: GarmanKohlhagen83 { s: 100.0, r_d: 0.05, r_f: 0.03, v: 0.2 }
// Option: EuropeanVanillaOption { strike: 100.0, expiry: 2025-12-31, type_flag: Call }
// {
// "ultima": -43.59776593173644,
// "vega": 39.6121492700665,
// "theta": -4.272756285502488,
// "lambda": 6.204336819109864,
// "color": 0.009074941597741354,
// "charm": 0.01906616295796282,
// "rho": 52.084231395586315,
// "vanna": 5.2399933461312134e-17,
// "zomma": -0.08997722338863051,
// "price": 9.092954864173855,
// "gamma": 0.017995444677726104,
// "delta": 0.5641575465829798,
// "speed": -0.0003599088935545221,
// "vomma": -1.1534441205446944e-15,
// }
// Model: Heston93 { s: 100.0, v: 0.05, r: 0.03, q: 0.2, rho: 0.1, kappa: 0.1, theta: 0.1, sigma: 0.1 }
// Option: EuropeanVanillaOption { strike: 100.0, expiry: 2025-12-31, type_flag: Call }
// {
// "delta": 0.2008452387306263,
// "gamma": 0.010457662539600598,
// "price": 2.683032821893125,
// "rho": 19.152359760630095,
// }
// Model: Bachelier { f: 100.0, r: 0.05, v: 0.2 }
// Option: EuropeanVanillaOption { strike: 100.0, expiry: 2025-12-31, type_flag: Call }
// {
// "delta": 0.5,
// "vega": 0.4185313362945294,
// "gamma": 1.9013503803678706,
// "atm_price": 0.08370626725890587,
// "theta": -0.03802700760735742,
// "price": 0.079224298540133,
// }math
Numerical Integration
Here we integrate the Gaussian density, which integrates to 1:
\[
\int_{\mathbb{R}} \frac{1}{\sqrt{2 \pi}} e^{\left( -\frac{x^2}{2} \right)} dx = 1
\]
use std::f64::consts::PI;
use RustQuant::math::*;
fn main() {
// Define a function to integrate:
// Standard Normal Distribution PDF
fn f(x: f64) -> f64 {
(2. * PI).sqrt().recip() * (-0.5 * x.powi(2)).exp()
}
// Integrate from -5 to 5.
// This is: +/- 5 standard deviations from the mean.
let integral = integrate(f, -5., 5.);
// Standard Normal Distribution PDF has integral of 1.
println!("Integral = {}", integral); // ~= 1.0
}
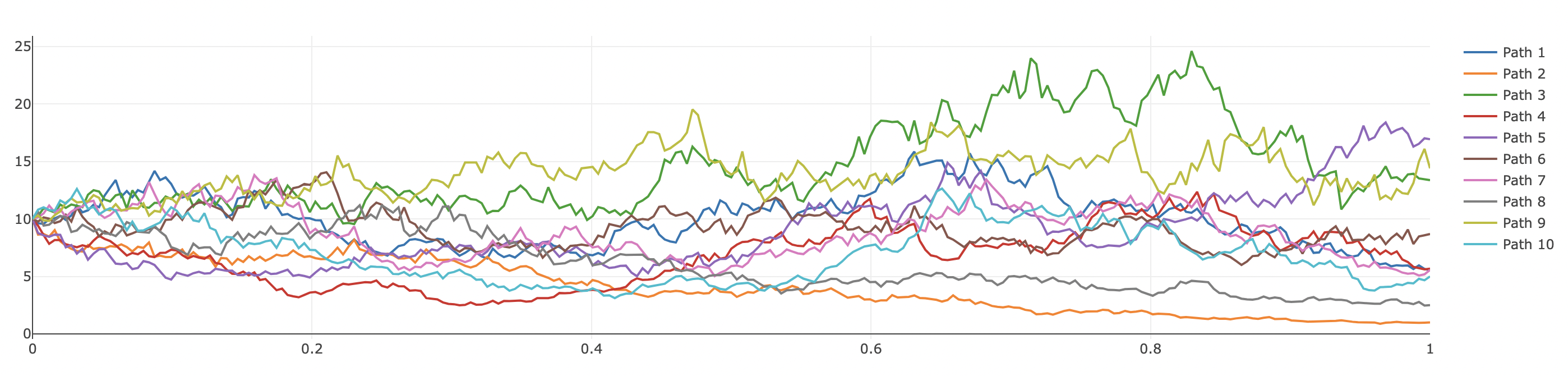
stochastics
Many stochastic processes can be generated:
// Run this example using:
// cargo run --example stochastic_processes
//
// This example generates paths for each stochastic process
// and plots them using the `plotters` crate.
//
// See the ./images/ directory for the output.
use RustQuant::stochastics::*;
// use RustQuant::utils::plot_vector;
const INITIAL_VALUE: f64 = 10.0;
const START_TIME: f64 = 0.0;
const END_TIME: f64 = 1.0;
const NUM_STEPS: usize = 252;
const NUM_SIMS: usize = 1;
const PARALLEL: bool = false;
#[rustfmt::skip]
fn main() {
// Create new stochastic processes.
let abm = ArithmeticBrownianMotion::new(0.05, 0.9);
let bdt = BlackDermanToy::new(0.13, 0.1);
let bm = BrownianMotion::new();
let cir = CoxIngersollRoss::new(0.05, 0.9, 0.1);
let ev = ExtendedVasicek::new(0.05, 2.0, 0.1);
let gbm = GeometricBrownianMotion::new(0.05, 0.9);
let hl = HoLee::new(0.2, 0.1);
let hw = HullWhite::new(0.1, 0.2, 0.1);
let ou = OrnsteinUhlenbeck::new(0.05, 0.9, 0.1);
let fbm = FractionalBrownianMotion::new(0.7, FractionalProcessGeneratorMethod::FFT);
let mjd = MertonJumpDiffusion::new(0.05, 0.5, 30.0, 0.0, 5.0);
let gbb = GeometricBrownianBridge::new(0.05, 0.9, INITIAL_VALUE, END_TIME);
let cev = ConstantElasticityOfVariance::new(0.05, 0.9, f64::sin);
// Generate path using Euler-Maruyama scheme.
// Parameters: x_0, t_0, t_n, n, sims, parallel.
let config = StochasticProcessConfig::new(
INITIAL_VALUE, START_TIME, END_TIME, NUM_STEPS, StochasticScheme::EulerMaruyama, NUM_SIMS, PARALLEL, None
);
let abm_out = abm.generate(&config);
let bdt_out = bdt.generate(&config);
let bm_out = bm.generate(&config);
let cir_out = cir.generate(&config);
let ev_out = ev.generate(&config);
let gbm_out = gbm.generate(&config);
let hl_out = hl.generate(&config);
let hw_out = hw.generate(&config);
let ou_out = ou.generate(&config);
let fbm_out = fbm.generate(&config);
let mjd_out = mjd.generate(&config);
let gbb_out = gbb.generate(&config);
let cev_out = cev.generate(&config);
// Plot the paths.
// plot_vector!(abm_out.paths[0].clone(), "./images/arithmetic_brownian_motion.png");
// plot_vector!(bdt_out.paths[0].clone(), "./images/black_derman_toy.png");
// plot_vector!(bm_out.paths[0].clone(), "./images/brownian_motion.png");
// plot_vector!(cir_out.paths[0].clone(), "./images/cox_ingersoll_ross.png");
// plot_vector!(ev_out.paths[0].clone(), "./images/extended_vasicek.png");
// plot_vector!(gbm_out.paths[0].clone(), "./images/geometric_brownian_motion.png");
// plot_vector!(hl_out.paths[0].clone(), "./images/ho_lee.png");
// plot_vector!(hw_out.paths[0].clone(), "./images/hull_white.png");
// plot_vector!(ou_out.paths[0].clone(), "./images/ornstein_uhlenbeck.png");
// plot_vector!(fbm_out.paths[0].clone(), "./images/fractional_brownian_motion.png");
// plot_vector!(mjd_out.paths[0].clone(), "./images/merton_jump_diffusion.png");
// plot_vector!(gbb_out.paths[0].clone(), "./images/geometric_brownian_bridge.png");
// plot_vector!(cev_out.paths[0].clone(), "./images/constant_elasticity_of_variance.png");
plot_trajectories(&gbm_out, true);
}
Paths can be plotted via the plot_vector! macro or plotly:
Contributing to RustQuant
I'm particularly interested in hearing from people with strong experience in implementing quantitative software in a real-world/professional setting. This is irrespective of whether you're interested in Rust or not, I would simply love to get feedback and suggestions from experienced people.
If you're reading this, I assume you're interested in contributing to this project.
If so, thank you very much! I would love to grow the project and have a solid, stable library that can be used by many people.
Firstly, this contribution guide is a work in progress, so bare with me.
I welcome contributions of all kinds, including:
- Bug reports.
- Bug fixes.
- Feature requests.
- Feature implementations.
- Documentation improvements.
- Unit tests.
If you have any ideas, feel free to make an issue to discuss it, or just make a pull request.
Additionally, feel free to contact me directly at: RustQuantContact@gmail.com
If you decide to contribute, please include the following license header in any files you create:
#![allow(unused)] fn main() { // ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ // RustQuant: A Rust library for quantitative finance tools. // Copyright (C) 2023 https://github.com/avhz // Dual licensed under Apache 2.0 and MIT. // See: // - LICENSE-APACHE.md // - LICENSE-MIT.md // ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ }
The following tools are good to use before pushing, cargo build at a minimum:
cargo doc
cargo fmt
cargo clippy
cargo check
cargo test
cargo build
I also like to separate the code as below, as I think it improves the readability a lot, and I would encourage any PRs to do the same (or similar). Of course, any suggestions or opinions on different styles are welcome!
#![allow(unused)] fn main() { // ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ // Structs, enums, and traits // ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ enum Enum {} struct Struct {} trait Trait {} // ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ // Implementations, functions, and macros // ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ impl Struct {} impl Trait for Struct {} // ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ // Unit tests // ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ #[cfg(test)] mod tests { use super::*; #[test] fn very_thorough_test() {} } }
One last thing, add an entry with your @username to the CHANGELOG.md file so that people can see what you've done.
Thank you for your interest in contributing to RustQuant!
File Structure Template
This is explained in Contributing, but for ease of finding and copy-pasting, all .rs files should use the following template:
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
// RustQuant: A Rust library for quantitative finance tools.
// Copyright (C) 2023 https://github.com/avhz
// Dual licensed under Apache 2.0 and MIT.
// See:
// - LICENSE-APACHE.md
// - LICENSE-MIT.md
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
// IMPORTS
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
use RustQuant::*;
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
// STRUCTS, ENUMS, AND TRAITS
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
enum Enum {}
struct Struct {}
trait Trait {}
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
// IMPLEMENTATIONS, TRAITS, AND FUNCTIONS
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
impl Struct {}
impl Trait for Struct {}
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
// UNIT TESTS
// ~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
#[cfg(test)]
mod tests {
use super::*;
#[test]
fn very_thorough_test() {}
}References
Quantitative Finance
- John C. Hull - Options, Futures, and Other Derivatives
- Damiano Brigo & Fabio Mercurio - Interest Rate Models - Theory and Practice (With Smile, Inflation and Credit)
- Paul Glasserman - Monte Carlo Methods in Financial Engineering
- Steven E. Shreve - Stochastic Calculus for Finance II: Continuous-Time Models
- Espen Gaarder Haug - Option Pricing Formulas
- Antoine Savine - Modern Computational Finance: AAD and Parallel Simulations
- Jessica James & Nick Webber - Interest Rate Modelling
- Jim Gatheral - The Volatility Surface
- Lorenzo Bergomi - Stochastic Volatility Modelling
Mathematics
- Andreas Griewank & Andrea Walther - Evaluating Derivatives - Principles and Techniques of Algorithmic Differentiation
- Uwe Naumann - The Art of Differentiating Computer Programs: An Introduction to Algorithmic Differentiation
Rust
- S. Klabnik & C. Nichols - The Rust Programming Language
- J. Gjengset - Rust for Rustaceans
- J. Blandy - Rust Programming
Licenses
RustQuant is dual licensed under Apache Version 2.0 and MIT.
Apache Version 2.0 License
Apache License
Version 2.0, January 2004
http://www.apache.org/licenses/
TERMS AND CONDITIONS FOR USE, REPRODUCTION, AND DISTRIBUTION
1. Definitions.
"License" shall mean the terms and conditions for use, reproduction,
and distribution as defined by Sections 1 through 9 of this document.
"Licensor" shall mean the copyright owner or entity authorized by
the copyright owner that is granting the License.
"Legal Entity" shall mean the union of the acting entity and all
other entities that control, are controlled by, or are under common
control with that entity. For the purposes of this definition,
"control" means (i) the power, direct or indirect, to cause the
direction or management of such entity, whether by contract or
otherwise, or (ii) ownership of fifty percent (50%) or more of the
outstanding shares, or (iii) beneficial ownership of such entity.
"You" (or "Your") shall mean an individual or Legal Entity
exercising permissions granted by this License.
"Source" form shall mean the preferred form for making modifications,
including but not limited to software source code, documentation
source, and configuration files.
"Object" form shall mean any form resulting from mechanical
transformation or translation of a Source form, including but
not limited to compiled object code, generated documentation,
and conversions to other media types.
"Work" shall mean the work of authorship, whether in Source or
Object form, made available under the License, as indicated by a
copyright notice that is included in or attached to the work
(an example is provided in the Appendix below).
"Derivative Works" shall mean any work, whether in Source or Object
form, that is based on (or derived from) the Work and for which the
editorial revisions, annotations, elaborations, or other modifications
represent, as a whole, an original work of authorship. For the purposes
of this License, Derivative Works shall not include works that remain
separable from, or merely link (or bind by name) to the interfaces of,
the Work and Derivative Works thereof.
"Contribution" shall mean any work of authorship, including
the original version of the Work and any modifications or additions
to that Work or Derivative Works thereof, that is intentionally
submitted to Licensor for inclusion in the Work by the copyright owner
or by an individual or Legal Entity authorized to submit on behalf of
the copyright owner. For the purposes of this definition, "submitted"
means any form of electronic, verbal, or written communication sent
to the Licensor or its representatives, including but not limited to
communication on electronic mailing lists, source code control systems,
and issue tracking systems that are managed by, or on behalf of, the
Licensor for the purpose of discussing and improving the Work, but
excluding communication that is conspicuously marked or otherwise
designated in writing by the copyright owner as "Not a Contribution."
"Contributor" shall mean Licensor and any individual or Legal Entity
on behalf of whom a Contribution has been received by Licensor and
subsequently incorporated within the Work.
2. Grant of Copyright License. Subject to the terms and conditions of
this License, each Contributor hereby grants to You a perpetual,
worldwide, non-exclusive, no-charge, royalty-free, irrevocable
copyright license to reproduce, prepare Derivative Works of,
publicly display, publicly perform, sublicense, and distribute the
Work and such Derivative Works in Source or Object form.
3. Grant of Patent License. Subject to the terms and conditions of
this License, each Contributor hereby grants to You a perpetual,
worldwide, non-exclusive, no-charge, royalty-free, irrevocable
(except as stated in this section) patent license to make, have made,
use, offer to sell, sell, import, and otherwise transfer the Work,
where such license applies only to those patent claims licensable
by such Contributor that are necessarily infringed by their
Contribution(s) alone or by combination of their Contribution(s)
with the Work to which such Contribution(s) was submitted. If You
institute patent litigation against any entity (including a
cross-claim or counterclaim in a lawsuit) alleging that the Work
or a Contribution incorporated within the Work constitutes direct
or contributory patent infringement, then any patent licenses
granted to You under this License for that Work shall terminate
as of the date such litigation is filed.
4. Redistribution. You may reproduce and distribute copies of the
Work or Derivative Works thereof in any medium, with or without
modifications, and in Source or Object form, provided that You
meet the following conditions:
(a) You must give any other recipients of the Work or
Derivative Works a copy of this License; and
(b) You must cause any modified files to carry prominent notices
stating that You changed the files; and
(c) You must retain, in the Source form of any Derivative Works
that You distribute, all copyright, patent, trademark, and
attribution notices from the Source form of the Work,
excluding those notices that do not pertain to any part of
the Derivative Works; and
(d) If the Work includes a "NOTICE" text file as part of its
distribution, then any Derivative Works that You distribute must
include a readable copy of the attribution notices contained
within such NOTICE file, excluding those notices that do not
pertain to any part of the Derivative Works, in at least one
of the following places: within a NOTICE text file distributed
as part of the Derivative Works; within the Source form or
documentation, if provided along with the Derivative Works; or,
within a display generated by the Derivative Works, if and
wherever such third-party notices normally appear. The contents
of the NOTICE file are for informational purposes only and
do not modify the License. You may add Your own attribution
notices within Derivative Works that You distribute, alongside
or as an addendum to the NOTICE text from the Work, provided
that such additional attribution notices cannot be construed
as modifying the License.
You may add Your own copyright statement to Your modifications and
may provide additional or different license terms and conditions
for use, reproduction, or distribution of Your modifications, or
for any such Derivative Works as a whole, provided Your use,
reproduction, and distribution of the Work otherwise complies with
the conditions stated in this License.
5. Submission of Contributions. Unless You explicitly state otherwise,
any Contribution intentionally submitted for inclusion in the Work
by You to the Licensor shall be under the terms and conditions of
this License, without any additional terms or conditions.
Notwithstanding the above, nothing herein shall supersede or modify
the terms of any separate license agreement you may have executed
with Licensor regarding such Contributions.
6. Trademarks. This License does not grant permission to use the trade
names, trademarks, service marks, or product names of the Licensor,
except as required for reasonable and customary use in describing the
origin of the Work and reproducing the content of the NOTICE file.
7. Disclaimer of Warranty. Unless required by applicable law or
agreed to in writing, Licensor provides the Work (and each
Contributor provides its Contributions) on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or
implied, including, without limitation, any warranties or conditions
of TITLE, NON-INFRINGEMENT, MERCHANTABILITY, or FITNESS FOR A
PARTICULAR PURPOSE. You are solely responsible for determining the
appropriateness of using or redistributing the Work and assume any
risks associated with Your exercise of permissions under this License.
8. Limitation of Liability. In no event and under no legal theory,
whether in tort (including negligence), contract, or otherwise,
unless required by applicable law (such as deliberate and grossly
negligent acts) or agreed to in writing, shall any Contributor be
liable to You for damages, including any direct, indirect, special,
incidental, or consequential damages of any character arising as a
result of this License or out of the use or inability to use the
Work (including but not limited to damages for loss of goodwill,
work stoppage, computer failure or malfunction, or any and all
other commercial damages or losses), even if such Contributor
has been advised of the possibility of such damages.
9. Accepting Warranty or Additional Liability. While redistributing
the Work or Derivative Works thereof, You may choose to offer,
and charge a fee for, acceptance of support, warranty, indemnity,
or other liability obligations and/or rights consistent with this
License. However, in accepting such obligations, You may act only
on Your own behalf and on Your sole responsibility, not on behalf
of any other Contributor, and only if You agree to indemnify,
defend, and hold each Contributor harmless for any liability
incurred by, or claims asserted against, such Contributor by reason
of your accepting any such warranty or additional liability.
END OF TERMS AND CONDITIONS
APPENDIX: How to apply the Apache License to your work.
To apply the Apache License to your work, attach the following
boilerplate notice, with the fields enclosed by brackets "[]"
replaced with your own identifying information. (Don't include
the brackets!) The text should be enclosed in the appropriate
comment syntax for the file format. We also recommend that a
file or class name and description of purpose be included on the
same "printed page" as the copyright notice for easier
identification within third-party archives.
Copyright 2023 https://github.com/avhz
Licensed under the Apache License, Version 2.0 (the "License");
you may not use this file except in compliance with the License.
You may obtain a copy of the License at
http://www.apache.org/licenses/LICENSE-2.0
Unless required by applicable law or agreed to in writing, software
distributed under the License is distributed on an "AS IS" BASIS,
WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
See the License for the specific language governing permissions and
limitations under the License.
MIT License
Copyright 2023 https://github.com/avhz
Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the “Software”), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED “AS IS”, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.